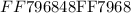Question

on a horizontal line segment, point A is located at 21, point b is located at 66. point p is a point that divides segment ab in a ratio of 3:2 from a to b where is point p located

Answer 1

We have a one-dimensional horizontal line segment. Three points are indicated on the line as follows:

In the above sketch we have first denoted a reference point at the extreme left hand as ( Ref = 0 ). This is classified as the origin. The point ( A ) is located on the same line and is at a distance of ( 21 units ) from Reference ( Ref ). The point ( B ) is located on the same line and is at a distance of ( 66 units ) from Reference ( Ref ).

The point is located on the line segment ( AB ) in such a way that it given as ratio of length of line segment ( AB ). The ratio of point ( P ) from point ( A ) and from ( P ) to ( B ) is given as:

`\textcolor{#FF7968}{(AP)/(PB)}\text{\textcolor{#FF7968}{ = }}\textcolor{#FF7968}{(3)/(2)\ldots}\text{\textcolor{#FF7968}{ Eq1}}`

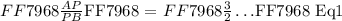
The length of line segment ( AB ) can be calculated as follows:

`\begin{gathered} AB\text{ = OB - OA } \\ AB\text{ = ( 66 ) - ( 21 ) } \\ \textcolor{#FF7968}{AB}\text{\textcolor{#FF7968}{ = 45 units}} \end{gathered}`

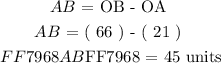
We can form a relation for the line segment ( AB ) in terms of segments related to point ( P ) as follows:

`\begin{gathered} \textcolor{#FF7968}{AB}\text{\textcolor{#FF7968}{ = AP + PB }}\textcolor{#FF7968}{\ldots}\text{\textcolor{#FF7968}{ Eq2}} \\ \end{gathered}`

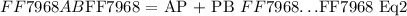
We were given a ratio of line segments as ( Eq1 ) and we developed an equation relating the entire line segment ( AB ) in terms two smaller line segments as ( Eq2 ).

We have two equation that we can solve simultaneously:

`\begin{gathered} \textcolor{#FF7968}{(AP)/(PB)}\text{\textcolor{#FF7968}{ = }}\textcolor{#FF7968}{\frac{3}{2\text{ }}\ldots}\text{\textcolor{#FF7968}{ Eq1}} \\ \textcolor{#FF7968}{AB}\text{\textcolor{#FF7968}{ = AP + PB }}\textcolor{#FF7968}{\ldots Eq2} \end{gathered}`

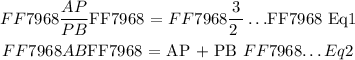
Step 1: Use Eq1 and express AP in terms of PB.

`AP\text{ = }(3)/(2)\cdot PB`

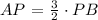
Step 2: Substitute ( AP ) in terms of ( PB ) into Eq2

`AB\text{ = }(3)/(2)\cdot PB\text{ + PB}`

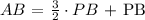
We already determined the length of the line segment ( AB ). Substitute the value in the above expression and solve for ( PB ).

Step 3: Solve for PB

`\begin{gathered} 45\text{ = }(5)/(2)\cdot PB \\ \textcolor{#FF7968}{PB}\text{\textcolor{#FF7968}{ = 18 units}} \end{gathered}`

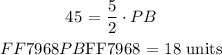
Step 4: Solve for AP

`\begin{gathered} AP\text{ = }(3)/(2)\cdot\text{ ( 18 )} \\ \textcolor{#FF7968}{AP}\text{\textcolor{#FF7968}{ = 27 units}} \end{gathered}`

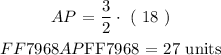
Step 5: Locate the point ( P )

All the points on the line segment are located with respect to the Reference of origin ( Ref = 0 ). We will also express the position of point ( P ).

Taking a look at point ( P ) in the diagram given initially we can augment two line segments ( OA and AP ) as follows:

`\begin{gathered} OP\text{ = OA + AP} \\ OP\text{ = 21 + 27} \\ \textcolor{#FF7968}{OP}\text{\textcolor{#FF7968}{ = 48 units}} \end{gathered}`

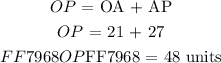
The point ( P ) is located at.

Answer:

`\textcolor{#FF7968}{48}\text{\textcolor{#FF7968}{ }}`