Question

3. For the polynomial: ()=−2(+19)3(−14)(+3)2, do the following:A. Create a table of values that have the x-intercepts of p(x) in the first column and their multiplicities in the second column.B. State the degree and end behavior for p(x). C. Hand sketch a rough graph of p(x). You should have the x-int labeled, but you do not need tick marks for all numbers in between.

Answer 1

Part A. We are given the following polynomial:

`\mleft(\mright)=-2\mleft(+19\mright)^3\mleft(-14\mright)\mleft(+3\mright)^2`

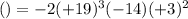
This is a polynomial of the form:

`p=k(x-a)^b(x-c)^d\ldots(x-e)^f`

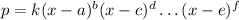
The x-intercepts are the numbers that make the polynomial zero, that is:

`\begin{gathered} p=0 \\ (x-a)^b(x-c)^d\ldots(x-e)^f=0 \end{gathered}`

The values of x are then found by setting each factor to zero:

`\begin{gathered} (x-a)=0 \\ (x-c)=0 \\ \text{.} \\ \text{.} \\ (x-e)=0 \end{gathered}`

Therefore, this values are:

`\begin{gathered} x=a \\ x=c \\ \text{.} \\ \text{.} \\ x=e \end{gathered}`

In this case, the x-intercepts are:

`\begin{gathered} x=-19 \\ x=14 \\ x=-3 \end{gathered}`

The multiplicity are the exponents of the factor where we got the x-intercept, therefore, the multiplicities are:

Part B. The degree of a polynomial is the sum of its multiplicities, therefore, the degree in this case is:

`\begin{gathered} n=3+1+2 \\ n=6 \end{gathered}`

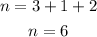
To determine the end behavior of the polynomial we need to know the sign of the leading coefficient that is, the sign of the coefficient of the term with the highest power. In this case, the leading coefficient is -2, since the degree of the polynomial is an even number this means that both ends are down. If the leading coefficient were a positive number then both ends would go up. In the case that the leading coefficient was positive and the degree and odd number then the left end would be down and the right end would be up, and if the leading coefficient were a negative number and the degree an odd number then the left end would be up and the right end would be down.

Part C. A sketch of the graph is the following:

If the multiplicity is an odd number the graph will cross the x-axis at that x-intercept and if the multiplicity is an even number it will tangent to the x-axis at that x-intercept.