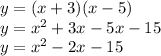Question

Please show the work

Answer 1

`A.f(x) = x^(2) -2x - 15`

Explanation:

Based on the given information, one can write the quadratic equation in factored form. Since the zeros of the equation are the roots, one can say that;

`y = ( x + 3 )( x - 5)`

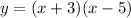
(where x = -3, and x = 5 are the roots)

Now all one has to do is distribute to find the quadratic equation in standard form;

`y = (x + 3) (x - 5)\\y = x^(2) +3x - 5x - 15\\y = x^(2) -2x - 15`