The two groups are given one is those who are studied and other is those who are not studied.
Studied - 88,100,94,79,92,100,95,83,89,99,100,91,89,95,100,93,96,84.
Arrange in order.
79, 83, 84, 88, 89, 89, 91, 92, 93, 94, 95, 95, 96, 99, 100, 100, 100, 100
The mean of this group is
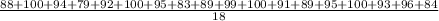
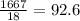
The mean is 92.6.
The median of this group is
Use the median formula for even
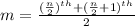
Substitute the value of n =18
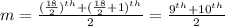
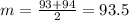
The median is 93.5.
The mode of this group is 100 as it is appears 3 times .
The another group is not studied group.
Not studied - 82,72,45,91,58,83,65,87,90,77,73,89.
Arrange in order-
45, 58, 65, 72, 73, 77, 82, 83, 87, 89, 90, 91
The mean is determined as
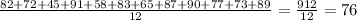
The median is determined as
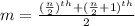
Substitute n=12.
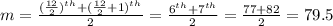
There is no mode.
So, from the all the data given.
The mean of the group that studied is over 15 percent points higher than the mean of the group that did not studied.
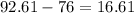
The median of the group that did not studied is less than 80.
In general , those students that studied scored much higher than those students that did not study.
The correct options are a , c and e.