Question

Three ballet dancers are positioned on stage. Jada is 2 meters straight behind Trisha and 4 meters directly left of Ken. When the music begins, Jada twirls to Ken's position, then leaps to Trisha's position, and finally walks back to her original position. How far did Jada travel? If necessary, round to the nearest tenth.

Answer 1

10.5 meters

Explanation:

in their starting position all three dancers form a right triangle with legs equal to 2m and 4m.

Jada to Ken = 4m

From Ken's position to Trisha's, Jada goes another 2
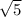`√(5)`m*

From Trisha's position to her original position, Jada goes another 2m

* to get this value: 2² + 4² = x²

x² = √20 = 2√5