we have
49x^2 + 16y^2 - 392x +160y + 400 = 0
Complete the square
Group terms
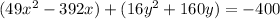
Factor 49 and 16
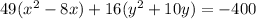
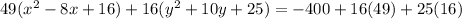
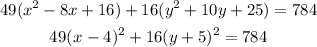
Divide by 784 both sides
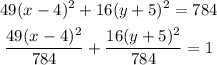
simplify
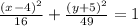
we have a vertical elipse
the center is the point (4,-5)
major semi axis is 7
we have
a^2=16 --------> a=4
b^2=49 ------> b=7
Find the value of c
![\begin{gathered} c=\sqrt[]{b^2-a^2} \\ c=\sqrt[]{33} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ninkvmls311fdge7rsxe.png)
see the attached figure to better understand the problem