Question

49x^2 + 16y^2 - 392x +160y + 400 = 01. give the coordinates of the upper vertex2. give the coordinates of the lower vertex3. give the coordinates of the upper focus(round to the nearest hundredths)4. give the coordinates of the lower focus(round to the nearest hundredths)5. give the eccentricity

Answer 1

we have

49x^2 + 16y^2 - 392x +160y + 400 = 0

Complete the square

Group terms

`(49x^2-392x)+(16y^2+160y)=-400`

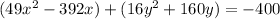
Factor 49 and 16

`49(x^2-8x)+16(y^2+10y)=-400`
`49(x^2-8x+16)+16(y^2+10y+25)=-400+16(49)+25(16)`
`\begin{gathered} 49(x^2-8x+16)+16(y^2+10y+25)=784 \\ 49(x^{}-4)^2+16(y+5)^2=784 \end{gathered}`

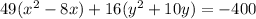
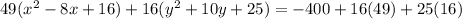
Divide by 784 both sides

`\begin{gathered} 49(x^{}-4)^2+16(y+5)^2=784 \\ \frac{49(x^{}-4)^2}{784}+(16(y+5)^2)/(784)=1 \end{gathered}`

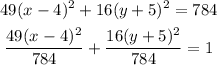
simplify

`\frac{(x^{}-4)^2}{16}+((y+5)^2)/(49)=1`

we have a vertical elipse

the center is the point (4,-5)

major semi axis is 7

we have

a^2=16 --------> a=4

b^2=49 ------> b=7

Find the value of c

`\begin{gathered} c=\sqrt[]{b^2-a^2} \\ c=\sqrt[]{33} \end{gathered}`

see the attached figure to better understand the problem