Question

Find the area bounded by the graphs of

Answer 1

(9ln(3) -6)/4 ≈ 0.97187765

Explanation:

A horizontal slice of the area will range from g^-1(y) to f^-1(y). The inverse functions are ...

f^-1(x) = 1/2·ln(x)

g^-1(x) = -1/4·ln(x)

Then the integral can be written as ...

`\displaystyle A=\int_1^3{\left((1)/(2)\ln(y)-(-1)/(4)\ln(y)\right)}\,dy=(3)/(4)\int_1^3{\ln(y)}\,dy=(3)/(4)\left.(xln((x))-x)\right|_1^3\\\\=(3)/(4)(3\ln(3)-(3-1))=\boxed{(9\ln(3)-6)/(4)\approx0.97187765}`

__

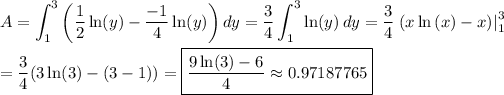
The attachment shows a numerical integration using a vertical slice of area. The result is identical to 12 significant figures.