Question

the ratio of the side of two similar cubes is 3:4 the smaller cube has a volume of 729 what is the volume of the larger cube

Answer 1

lemme see, notice, this is the relationship from side ratios,
to areas and volumes
keep in mind that areas are square figures, involving 2 units,
and volumes are cubic figures, involving 3 units
thus
`\bf \begin{array}{llll} &ratio&relationship\\ lenght&3:4&\cfrac{3}{4}=\cfrac{s}{s}\\\\ area&3:4&\left( \cfrac{3}{4} \right)^2=\cfrac{s^2(area)}{s^2(area)}\\\\ volume&3:4&\left( \cfrac{3}{4} \right)^3=\cfrac{s^3(volume)}{s^3(volume)} \end{array}`

what the dickens all that means?

well, you have two cubes, both similar, their ratio, is 3:4,
3 is smaller than 4, thus is from smaller to bigger cube, 3:4 ratio

the smaller cube has a volume, or
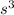
`s^3` of 729 cubic units,
what's the other volume?

well, let us use those proportions above
`\bf \left( \cfrac{3}{4} \right)^3=\cfrac{729}{v}\implies \cfrac{3^3}{4^3}=\cfrac{729}{v}`

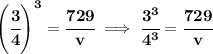
solve for "v"

notice, the numerator in 3:4, has the smaller volume, 729,
the bigger is at the bottom of that proportion