Question

20 POINTS HELP The figure shown is a square with a triangular hole cut into one side. The ratio of the height (h) of the triangle to a side length of the square is 7 to 8. The ratio of the base (b) of the triangle to the side length of the square is 1 to 2. If the area of the square is 64 square inches, what is the area of the shaded part of the square? Show you work.

Answer 1

it is 50 because you have to subtract the area of the triangle (14) from the area of the square (64)

Answer 2

Answer: Area of shaded part is 50 cm².

Explanation:

Since we have given that

Ratio of height of triangle to side length of the square is 7:8.

Let height of triangle be 'h'.

Let the length of square be 'a'.

Let the base of triangle be 'b'.

Ratio of base of triangle to side length of the square is 1:2.

So, Combined ratio will be

h : a : b

7 : 8

4(2 : 1) (to make 'a' as a common part which is 8 )

= 8 : 4

----------------------------------

7 : 8 : 4

So, height will be 7x.

Side will be 8x.

Base will be 4x.

Since area of square = 64 cm²

As we know that "Area of square = Side × Side":

`64=(8x)^2\\\\64=64x^2\\\\x^2=1\\\\x=1(\text{negative value will be discarded})`

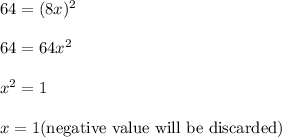
So, base becomes 4 inches.

Height becomes 7 inches.

So, Area of triangle becomes

`Area=(1)/(2)* base* height\\\\Area=(1)/(2)* 7* 4\\\\Area=2* 7\\\\Area=14\ cm^2`

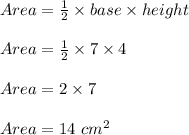
Area of shaded part of the square is

Area of square - Area of triangle

`=64-14\\\\=50\ cm^2`

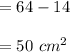
Hence, Area of shaded part is 50 cm².