Question

On a piece of paper, use a protractor to construct right triangle ABC with AB=3 in. , m∠A=90° , and m∠B=45° .

Answer 1

AC=3 in, m∠C=45° and BC=3√2 in.

Explanation:

Given information: ABC is a right angled triangle AB=3 in. , m∠A=90° , and m∠B=45° .

According to the angle sum property the sum of interior angles of a triangle is 180°.

`\angle A+\angle B+\angle C=180^(\circ)`

`90^(\circ)+45^(\circ)+\angle C=180^(\circ)`

`135^(\circ)+\angle C=180^(\circ)`

`\angle C=180^(\circ)-135^(\circ)`

`\angle C=45^(\circ)`

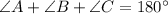
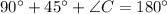
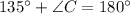
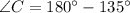
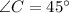
The measure of angle C is 45°.

In a right angled triangle,

`\tan\theta=(opposite)/(adjacent)`

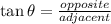
In triangle ABC,

`\tan B=(AC)/(AB)`

`\tan (45^(\circ))=(AC)/(3)`

`1=(AC)/(3)`

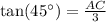
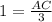
Multiply both sides by 3.

`3=AC`

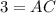
The measure of AC is 3 in.

According to Pythagoras theorem,

`hypotenuse^2=base^2+perpendicular^2`

`BC^2=3^2+3^2`

`BC^2=9+9`

`BC^2=18`

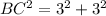
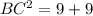
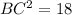
Taking square root on both sides.

`BC=√(18)`

`BC=3√(2)`

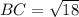
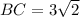
Therefore, the missing measurements are AC=3 in, m∠C=45° and BC=3√2 in.

Answer 2

AC = 3 in.

Explanation:

It is given in the figure attached, in Δ ABC

∠ A = 90°

m∠B = 45°

AB = 3 in.

We have to find all sides of the triangle given

we will apply sine in Δ ABC to find the measure of AC

sinB =
`(AB)/(BC)`

`sin45=(3)/(BC)`

`(1)/(√(2))=(3)/(BC)`

Now by cross multiplication

BC = 3√2 in.

Now by Pythagoras theorem

BC²= AC² + AB²

(3√2)² = AC² + 3²

18 - 9 = AC²

AC = √9 = 3

Now we come to the options you have mentioned

AC = 3 in. is the correct answer.