Question

Assume that a sample is used to estimate a population mean μ . Find the 99% confidence interval for a sample of size 891 with a mean of 20.8 and a standard deviation of 17.6. Enter your answer as a tri-linear inequality accurate to 3 decimal places.19.281Incorrect < μ < 22.319

Answer 1

The confidence interval is expressed as

where

`\begin{gathered} \bar{x}\text{ or }\mu\Rightarrow sample\text{ mean} \\ z\Rightarrow confidence\text{ level value} \\ s\Rightarrow sample\text{ standard deviation} \\ n\Rightarrow sample\text{ size} \end{gathered}`

Given a 99% confidence interval for a sample size of 891 with a mean of 20.8 and a standard deviation of 17.6, this implies that

`\begin{gathered} \bar{x}=20.8 \\ s=17.6 \\ n=891 \\ z=2.576 \end{gathered}`

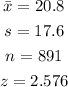
By substituting these values into the above equation, we have

`\begin{gathered} CI=20.8\pm(2.576*(17.6)/(√(891))) \\ =20.8\pm1.518866748 \\ Thus,\text{ } \\ \Rightarrow lower\text{ bound:} \\ 20.8-1.518866748=19.28113325 \\ \Rightarrow upper\text{ bound:} \\ 20.8+1.518866748=22.31886675 \end{gathered}`

Hence, we have

`19.281<\mu<22.319`