Explanation
We are required to determine the coordinates of W’X’Y’Z' when WXYZ is reflected across the line y = x.
This is achieved thus:
From the image, we can deduce the following:
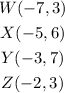
We know that the following reflection rules exist:
Therefore, we have:
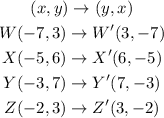
Hence, the answers are:

This is shown in the graph bwlow for further undertanding: