Answer:
(9ln(3) -6)/4 ≈ 0.97187765
Explanation:
A horizontal slice of the area will range from g^-1(y) to f^-1(y). The inverse functions are ...
f^-1(x) = 1/2·ln(x)
g^-1(x) = -1/4·ln(x)
Then the integral can be written as ...
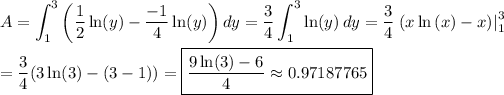
__
The attachment shows a numerical integration using a vertical slice of area. The result is identical to 12 significant figures.