Question

A 500 gallon tank initially contains 200 gallons of water with 5 lbs of salt dissolved in it. Water enters the tank at a rate of 2 gal/hr and the water entering the tank has a salt concentration 1/5 (1+ cos t) of lbs/gal. If a well-mixed solution leaves the tank at a rate of 2 gal/hr, how much salt is in the rank when it overflows?

Answer 1

Until the concerns I raised in the comments are resolved, you can still set up the differential equation that gives the amount of salt within the tank over time. Call it
`A(t)`.

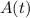
Then the ODE representing the change in the amount of salt over time is


`(\mathrm dA)/(\mathrm dt)=\text{rate in}-\text{rate out}`

`(\mathrm dA)/(\mathrm dt)=\frac{2\text{ gal}}{1\text{ hr}}*\frac{\frac15(1+\cos t)\text{ lbs}}{1\text{ gal}}-\frac{2\text{ gal}}{1\text{ hr}}*\frac{A(t)\text{ lbs}}{500+(2-2)t}`

`(\mathrm dA)/(\mathrm dt)=\frac25(1+\cos t)-\frac1{250}A(t)`

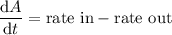
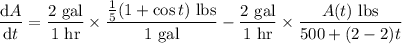
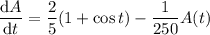
and this with the initial condition
`A(0)=5`

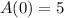
You have


`(\mathrm dA)/(\mathrm dt)+\frac1{250}A(t)=\frac25(1+\cos t)`

`e^(t/250)(\mathrm dA)/(\mathrm dt)+\frac1{250}e^(t/250)A(t)=\frac25e^(t/250)(1+\cos t)`

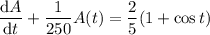
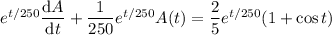
`(\mathrm d)/(\mathrm dt)\left[e^(t/250)A(t)\right]=\frac25e^(t/250)(1+\cos t)`

Integrating both sides gives


`e^(t/250)A(t)=100e^(t/250)\left(1+\frac1{62501}\cos t+(250)/(62501)\sin t\right)+C`

`A(t)=100\left(1+\frac1{62501}\cos t+(250)/(62501)\sin t\right)+Ce^(-t/250)`

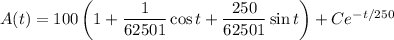
Since
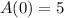
`A(0)=5`, you get


`5=100\left(1+\frac1{62501}\right)+C\implies C=-(5937695)/(62501)`

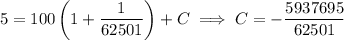
so the amount of salt at any given time in the tank is


`A(t)=100\left(1+\frac1{62501}\cos t+(250)/(62501)\sin t\right)-(5937695)/(62501)e^(-t/250)`

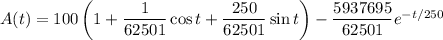
The tank will never overflow, since the same amount of solution flows into the tank as it does out of the tank, so with the given conditions it's not possible to answer the question.

However, you can make some observations about end behavior. As
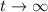
`t\to\infty`, the exponential term vanishes and the amount of salt in the tank will oscillate between a maximum of about 100.4 lbs and a minimum of 99.6 lbs.