Question

Given the system of equations, what is the solution? 5x - 4y = 7 x = 5 - 3/2 y

A. {(61/23, 36/23)}
B. {(-61/23, 36/23)}
c. {(61/23, -36/23)}

Answer 1

The answer is A


You can solve this by equation the two equations, by substitution method or elimination. Let's choose the substitution since Equation 2 has already X isolated
-take the X in equation 2 and substitute in the first equation
So, You should have 5 (5-3/2 y) -4y =7
Get y ( I'll assume you know how to simplify and find y by yourself )
y=36/23
-Now take y and substitute it in the first equation or the second equation (it doesn't really matter)
Substituting y in Equation 2:
x=5- 3/2 (36/23)
=> x= 61/23

So answer is A where (x,y) is (61/23, 36/23)

Answer 2

Option A is correct.

Explanation:

Given system of equations are

5x - 4y = 7 ...............(1)

x = 5 - 3/2y .................(2)

value of x from equation (2), put in equation (1)

`5(5-(3)/(2)y)-4y=7`

`25-(15)/(2)y-4y=7`

`-(15)/(2)y-(8)/(2)y=7-25`

`(-15-8)/(2)y=-18`

`(-23)/(2)y=-18`

`y=-18*(-2)/(23)`

`y=(36)/(23)`

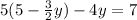
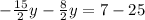
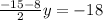
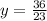
Now, Value of x =
`5-(3)/(2)*(36)/(23)=5-(54)/(23)=(115-54)/(23)=(61)/(23)`

Solution of given system is
`((61)/(23),(36)/(23))`

Therefore, Option A is correct.