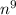Simplify. n 6 · n 5 ÷ n 4 · n 3 ÷ n 2 · n

Question

asked Sep 27, 2018 204k views

2 Answers

Kendon · Answer 1 · 2018-09-28T05:42:54+0000

Answer:

The given expression
$n^6\cdot n^5/ n^4\cdot n^3/ n^2\cdot n$ is

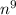
Explanation:

Given : Expression
$n^6\cdot n^5/ n^4\cdot n^3/ n^2\cdot n$

We have to write the simplified form for the given expression
$n^6\cdot n^5/ n^4\cdot n^3/ n^2\cdot n$

Consider the given expression
$n^6\cdot n^5/ n^4\cdot n^3/ n^2\cdot n$

Rewrite it in simpler form, we have,

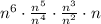
$n^6\cdot(n^5)/(n^4)\cdot (n^3)/(n^2)\cdot n$

Apply exponent rule,
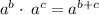$\:a^b\cdot \:a^c=a^(b+c)$ , we have,

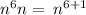
$n^6n=\:n^(6+1)$

$=(n^5)/(n^4)\cdot (n^3)/(n^2)n^(7)$

Apply exponent rule,
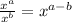
(x^a)/(x^b)=x^(a-b)

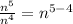
(n^5)/(n^4)=n^(5-4)

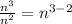
(n^3)/(n^2)=n^(3-2)

Expression becomes,

=n^7nn

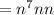
Again apply exponent rule, we have,

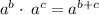
$\:a^b\cdot \:a^c=a^(b+c)$

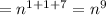
=n^(1+1+7)=n^9

Thus, The given expression
$n^6\cdot n^5/ n^4\cdot n^3/ n^2\cdot n$ is

Rob Potter · Answer 2 · 2018-10-02T09:52:54+0000

Answer:
n^(9)

Explanation:

Given expression:
$n^6\cdot n^5/ n^4\cdot n^3/ n^2\cdot n$

The law of exponents are given by :_

$a^m\cdot a^n=a^(m+n)\\\\a^m/ a^n=a^(m-n)$

Using PEDMAS, first we solve division, we get

$n^6\cdot n^(5-4)\cdot n^(3-2)\cdot n\\\\=n^6\cdot n\cdot n\cdot n$

Now, using product law of exponent we get

$n^(6+1+1+1)\\\\=n^(9)$