Question

Name four values of b which make the expression factorable:
x^2 - 3x + b

Answer 1

Four values that make the expression factorable will be, 2, -4, -18 and -28.

Answer 2

2, -4, -10 and -18.

Explanation:

The given expression is

`x^2-3x+b` ...(i)

We need to find the 4 values of b which make the expression factorable.

A polynomial is factorable if both roots are real.

If
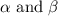`\alpha \text{ and }\beta` are two real roots of a polynomial, then the polynomial is defined as

`P(x)=x^2-(\alpha+\beta)x+\alpha\beta` ....(ii)

From (i) and (ii), we get

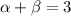`\alpha+\beta=3` ...(iii)

`\alpha\beta=b`

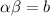
For equation (iii), possible pairs of
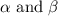`\alpha \text{ and }\beta` are (2,1), (4,-1), (5,-2) and (6,-3).

From these ordered pairs the values of b are

`b=\alpha\beta=2* 1=2`

`b=\alpha\beta=4* (-1)=-4`

`b=\alpha\beta=5* (-2)=-10`

`b=\alpha\beta=6* (-3)=-18`

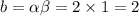
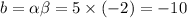
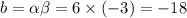
Therefore, the four possible values of b are 2, -4, -10 and -18.