Question

Michael wants to save $55,000.00 for a down payment on a home. How much will he need to invest in anaccount with 8.5% APR, compounding daily, in order to reach his goal in 3 years?

Answer 1

Step 1. The information that we have is:

The final amount that Michael wants to save is:

`A=55,000`

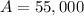
We will call that amount A.

The annual percentage rate of the investment, which we will label as r, is:

`r=8.5`

We will need this annual percentage rate represented as a decimal number, therefore, we divide it by 100:

`\begin{gathered} r=8.5/100 \\ r=0.085 \end{gathered}`

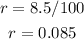
The time of the investment, t, is 3 years:

`t=3`

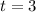
And it is compounded daily, let n be the number of times of compounding in a year:

`n=365`

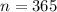
Step 2. We need to find the initial amount of the investment, which will be called P or principal.

The formula we will use to find it is:

`A=P(1+(r)/(n))^(nt)`

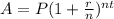
Step 3. Substituting the known values:

`55,000=P(1+(0.085)/(365))^((365)(3))`

From this equation, we need to solve the operations and solve for P, the principal amount of the investment.

Step 4. Simplifying the equation:

`55,000=P(1+0.0002328767)^(1095)`

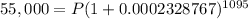
Continue simplifying:

`\begin{gathered} 55,000=P(1.0002328767)^(1,095) \\ 55,000=P(1.2904233) \end{gathered}`

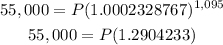
Then, we solve for P:

`\begin{gathered} (55,000)/(1.2904233)=P \\ 42,621.6726=P \end{gathered}`

Rounding to the nearest cent (2 decimal places) The amount that he needs to invest is $42,621.67

Answer: $42,621.67