Step 1. The information that we have is:
The final amount that Michael wants to save is:
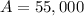
We will call that amount A.
The annual percentage rate of the investment, which we will label as r, is:
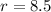
We will need this annual percentage rate represented as a decimal number, therefore, we divide it by 100:
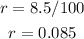
The time of the investment, t, is 3 years:
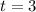
And it is compounded daily, let n be the number of times of compounding in a year:
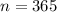
Step 2. We need to find the initial amount of the investment, which will be called P or principal.
The formula we will use to find it is:
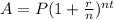
Step 3. Substituting the known values:
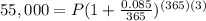
From this equation, we need to solve the operations and solve for P, the principal amount of the investment.
Step 4. Simplifying the equation:
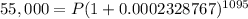
Continue simplifying:
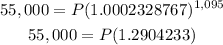
Then, we solve for P:
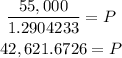
Rounding to the nearest cent (2 decimal places) The amount that he needs to invest is $42,621.67
Answer: $42,621.67