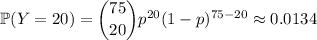Question

Scores on a test are normally distributed with a mean of 68.2 and a standard deviation of 10.4. Estimate the probability that among 75 randomly selscted students, at least 20 of them score greater that 78.

Answer 1

First, find the probability of scoring higher than 78. Scores are normally distributed, so you have


`\mathbb P(X>78)=\mathbb P\left((X-68.2)/(10.4)>(78-68.2)/(10.4)\right)\approx\mathbb P(Z>0.9423)\approx0.173`

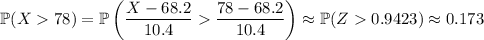
Now, the event that any given student scores higher than 78 follows a binomial distribution. Here you have 75 total students (so
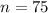
`n=75`) with success probability
`p=0.173`.

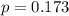
So the probability of getting 20 students that fit the criterion is


`\mathbb P(Y=20)=\dbinom{75}{20}p^(20)(1-p)^(75-20)\approx0.0134`