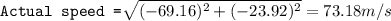Question

Robin rides a personal watercraft 75° west of south at 70 miles/hour. the water current is moving 6 miles/hour at an angle of 75° south of west. what is the actual speed (rounded to the nearest hundredth) of robin's watercraft?

Answer 1

Hi, thank you for posting your question here at Brainy.

The path of the watercraft and the water current, when joined by a line forming a right angle would make a right triangle. From here, we can know the component in which it is along the same direction with the watercraft. Let's denote this as x.

x = 6 miles/h * cos 75 degrees
x = 1.55 miles/h

Thus, the actual speed = 70 + 1.55 = 71.55 miles/h

Answer 2

Actual speed = 73.18 m/s

Explanation:

Let positive x axis represent east and positive y axis represent north.

Robin rides a personal watercraft 75° west of south at 70 miles/hour.

Velocity of personal watercraft = 70 miles/hour at 75° west of south

= 70 miles/hour at 15° south of west

= -70 cos 15 i + -70 sin 15 j

= -67.61 i - 18.12 j

The water current is moving 6 miles/hour at an angle of 75° south of west.

Velocity of water current = 6 miles/hour at 75° south of west

= 6 miles/hour at 75° south of west

= -6 cos 75 i + -6 sin 75 j

= -1.55 i - 5.80 j

Total velocity = -67.61 i - 18.12 j -1.55 i - 5.80 j = -69.16 i - 23.92 j

`\texttt{Actual speed =}√((-69.16)^2+(-23.92)^2)=73.18m/s`