Question

What is a growth factor in a table in a exponential function table and how to solve this math

Answer 1

(a) The growth factor is 1.9.

(b) The population after 10 and 15 years are 18393 and 455434 respectively.

(c)
`p=30(1.9)^n`

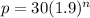
(d) In 17 years population exceed one million.

Explanation:

Given table represents an exponential function.

The general form of an exponential function is

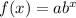`f(x)=ab^x` .... (1)

where, a is initial value and b is growth factor.

Consider any two point from the given table. (0,30) and (1,57).

`30=ab^0`

`30=a`

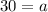
The value of a is 30.

`57=ab^1`

`57=30b`

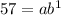
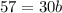
Divide both sides by 30.

`(57)/(30)=b`

`1.9=b`

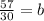
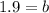
Substitute a=30 and b=1.9 in equation (1).

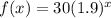`f(x)=30(1.9)^x` .... (2)

(a)

`b=1.9`

Therefore the growth factor is 1.9.

(b)

Substitute x=10 in equation (2), to find the population after 10 years.

`f(10)=30(1.9)^(10)`

`f(10)=18393.1987734`

`f(10)\approx 18393`

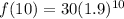
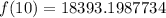
Therefore the population after 10 years is 18393.

Substitute x=15 in equation (2), to find the population after 15 years.

`f(15)=30(1.9)^(15)`

`f(15)=455433.810896`

`f(15)\approx 455434`

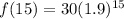
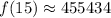
Therefore the population after 15 years is 455434.

(c)

The equation of elk population p for any year n after the elk were first counted is

`p=30(1.9)^n`

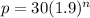
(d)

We need to find the number of years after that the population exceed one million.

Let in t years the population exceed one million.

`1000000<30(1.9)^t`

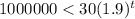
Divide both sides by 30.

`(100000)/(3)<(1.9)^t`

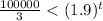
Taking ln both sides.

`\ln (100000)/(3)<\ln (1.9)^t`

`\ln (100000)/(3)<t\ln (1.9)`

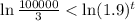
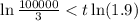
Divide both sides by ln(1.9).

`(\ln (100000)/(3))/(\ln (1.9))<t`

`16.2253643713<t`

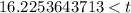
Therefore in 17 years population exceed one million.

Answer 2

You need to know the equation for an exponential from which is y=ab^x.

The a in the equation represents the y intercept or stating point, the b represent the growth factor or multiplier, and the x represents the exponent.

A) to find the growth factor, you what you are multiplying by to get the next number. So you are going from 30 to 57. Well, if you divide 57 by 30; you find out that you are multiplying by 1.9. So 1.9 is your growth factor.

B) I figured B is pretty much self explanatory since you now know your growth factor.

C) use the equation y=ab^x. Now substitute using the information you're given and you should get: y=30(1.9)^x.

D) you have you're equation so substitute the information you're given using your equation.