Question

The average turkey sold in the U.S. in 2005 weighed about 28 pounds, with a standard deviation of 3 pounds. The average in 1965 was 18 pounds, with a standard deviation of 2 pounds. At which time would it be more unusual to have a 23 pound turkey?

Answer 1

2005:
`\frac{23-28}3\approx-1.67`

1965:
`\frac{23-18}2=2.5`

Since the 23 lb turkey is closer to the 2005 mean and further from the 1965 mean, it would be more unusual to find such a turkey in 1965. (The closer the above values (z-scores) are to zero, the more likely they are to occur.)

Answer 2

In 1965

Explanation:

If in the normal distribution, z-scores is less than -1.96 or higher than 1.96 then it is considered to be unusual.

The mean weight in 2005,
`\mu_1=28`

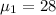
Standard deviation,
`\sigma_1=3`

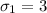
Also, if x represents average turkey sold ( in pounds ),

Then x = 23

So, z-score would be,

`z_1 =(x-\mu_1)/(\sigma_1)`

`=(23-28)/(3)`

`=-(5)/(3)`

`\approx -1.67`

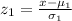
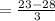
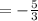
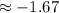
Now, mean weight in 165,
`\mu_2=18`

`\sigma=2`

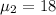
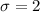
So, the z-score would be,

`z_2=(23-18)/(2)=(5)/(2)=2.5`

`\because | -1.96 - z_1 | < |1.96 - z_2 |`

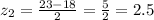
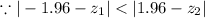
Hence, in 1965 it will be more unusual to have a 23 pound turkey.