Question

The Johnson twins were born eleven years after their older sister. This​ year, the product of the three​ siblings' ages is exactly 1181 more than the sum of their ages. How old are the​ twins?

Answer 1

So there are 3 siblings: the first twin, the second twin, and their older sister.

Since the sister is older by 11 years, you can represent their relationship with the following equation;
age of twin = age of older sister - 11
t = s - 11

Representing this next part may be a little hard to show, but i'll do my best :)

Adding the ages together can be represented like this;
total age = t + t + s
If the product of their ages ( t * t * s ) is 1181 more than the sum, you can show it like this:

`t * t * s = (t + t + s) + 1181`
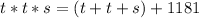
Now you substitute in (s - 11) for t because s = t - 11.

`t * t * s = (t + t + s) + 1181\\ (s-11) * (s-11) * s = ((s-11) + (s-11) + s) + 1181\\ (s^(2)-22x+121)*s=s+s-11-11+1181\\ s^(3)-22s^(2)+121s-2s=1159\\ s^(3)-22s^(2)+118s-1159=0`
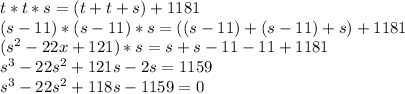
Factor:
Since it's a third-degree equation, I just entered it into a polynomial solver in my calculator. There was only one factor listed, x = 19. Using (s - 19) = 0 as a factor, the equation becomes the following:

`s^(3)-22s^(2)+118s-1159=0\\ (s-19)(s^(2)-3s+61)=0`
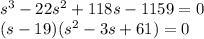
Using the quadratic formula, you get:

`s= \frac{-b(+-)\sqrt{b^(2)-4ac}}{2a}\\ s= \frac{-(-3)(+-)\sqrt{(-3)^(2)-4(1)(61)}}{2*1}\\ s= (3(+-)√((9)-244))/(2)\\ s= (3(+-)√(-235))/(2)`

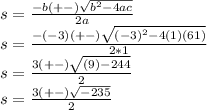
Since you have a square root of a negative number, the answer will be imaginary. You cannot have an age that is imaginary, so the age of the older sister (s) is 19 years.

Because t = s - 11, that means that t = (19) - 11 = 8.
t is the age of the twins, so the twins are 8 years old.