Question

Can y'all help me with number 6.

Answer 1

SOH CAH TOA ->
`\bf sin(\theta)=\cfrac{opposite}{hypotenuse} \qquad \qquad % cosine cos(\theta)=\cfrac{adjacent}{hypotenuse} \\ \quad \\ % tangent tan(\theta)=\cfrac{opposite}{adjacent}`

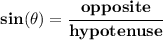
so.. which of those fellows do we use?
well, the triangle gives us

the angle, 15 degrees, for elevation angle
the adjacent side, 50m
and we want the opposite side, the slide

so...who has only, the angle, opposite, and adjacent sides?
well, low and behold, is Ms tangent
thus

`\bf tan(\theta)=\cfrac{opposite}{adjacent}\qquad \begin{cases} \theta\to 15^o\\ adjacent=50\\ opposite=x-15 \end{cases} \\ \quad \\ tan(15^o)=\cfrac{x-15}{50}\implies 50tan(15^o)=x-15\\\\ 50\cdot tan(15^o)+15=x`

notice, "x" in the picture, is the distance from the ground up to the top of the waterslide, using that triangle, what we're getting is just the distance, from the shorter slide, to the taller one, or x - 15
thus, the opposite side is x -15