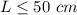Question

A rectangle with a width of 30cm has a perimeter from 100cm to 160cm. Graph a compound inequality that shows the possible lengths of the rectangle.

Part A: Use the number line below to graph the solution.
Part B. What type of compound inequality does your solution represent?
The Number line is from 0 to 100 in 10's

Answer 1

100 < perimeter < 160

Perimeter = 2(width + length)
100 < 2(width + length) < 160
50 < 30 + length < 80
20 < length < 50

This inequality shows the possible values of the length

Answer 2

Part A) The graph in the attached figure

Part B)
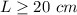`L\geq20\ cm` and
`L \leq 50\ cm`

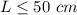
Explanation:

Part A)

we know that

The perimeter of a rectangle is equal to

`P=2(L+W)`

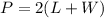
we have

`W=30\ cm`

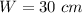
and the perimeter

`100\ cm \leq P\leq 160\ cm`

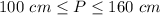
For
`P=100\ cm`

`100=2(L+30)`

`L=50-30=20\ cm`

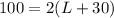
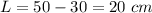
so

`L\geq20\ cm`

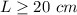
For
`P=160\ cm`

`160=2(L+30)`

`L=80-30=50\ cm`

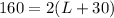
so

`L \leq 50\ cm`

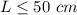
The solution of the possible lengths of the rectangle is the interval

`[20,50]`

All real numbers greater than or equal to
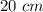`20\ cm` and less than or equal to
`50\ cm`

`20\ cm \leq L\leq 50\ cm`

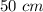
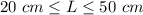
see the graph in the attached figure

Part B)

we know that

A compound inequality contains at least two inequalities that are separated by either "and" or "or". The graph of a compound inequality with an "and" represents the intersection of the graph of the inequalities.

In this problem

The compound inequality is equal to

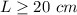`L\geq20\ cm` and
`L \leq 50\ cm`