Answer:
Option A is correct.
Lines AB and CD are parallel.
Explanation:
Parallel lines: They have the same slope and will never intersects.
Perpendicular lines : The slope of the perpendicular are negative reciprocal to each other.
As per the statement:
Line AB contains points A (0, 0) and B (2, 2).
Slope the two points is given by:
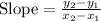
then;
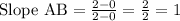
Similarly for:
Line CD contains points C (3, 1) and D (5, 3)
then;
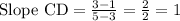
Since, the slope of AB = Slope of CD
then by definition:
⇒Lines AB and CD are parallel.