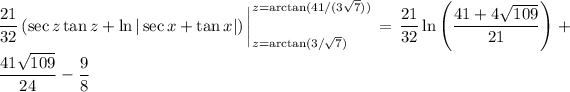Question

Let C be the curve of intersection of the parabolic cylinder x^2 = 2y, and the surface 3z = xy. Find the exact length of C from the origin to the point (4, 8, 32/3)

Answer 1

I've attached a plot of the intersection (highlighted in red) between the parabolic cylinder (orange) and the hyperbolic paraboloid (blue).

The arc length can be computed with a line integral, but first we'll need a parameterization for
`C`. This is easy enough to do. First fix any one variable. For convenience, choose
`x`.

Now,
`x^2=2y\implies y=\frac{x^2}2`, and
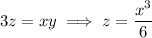
`3z=xy\implies z=\frac{x^3}6`. The intersection is thus parameterized by the vector-valued function


`\mathbf r(x)=\left\langle x,\frac{x^2}2,\frac{x^3}6\right\rangle`

where
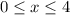
`0\le x\le 4`. The arc length is computed with the integral


`\displaystyle\int_C\mathrm dS=\int_0^4\|\mathbf r'(x)\|\,\mathrm dx=\int_0^4\sqrt{x^2+\frac{x^4}4+(x^6)/(36)}\,\mathrm dx`

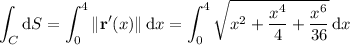
Some rewriting:


`\sqrt{x^2+\frac{x^4}4+(x^6)/(36)}=\sqrt{(x^2)/(36)}√(x^4+9x^2+36)=\frac x6√(x^4+9x^2+36)`

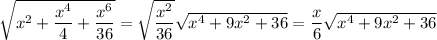
Complete the square to get


`x^4+9x^2+36=\left(x^2+\frac92\right)^2+\frac{63}4`

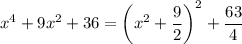
So in the integral, you can substitute
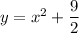
`y=x^2+\frac92` to get


`\displaystyle\frac16\int_0^4x\sqrt{\left(x^2+\frac92\right)^2+\frac{63}4}\,\mathrm dx=\frac1{12}\int_(9/2)^(41/2)\sqrt{y^2+\frac{63}4}\,\mathrm dy`

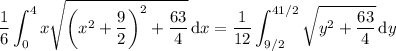
Next substitute
`y=\frac{√(63)}2\tan z`, so that the integral becomes


`\displaystyle\frac1{12}\int_(9/2)^(41/2)\sqrt{y^2+\frac{63}4}\,\mathrm dy=(21)/(16)\int_(\arctan(3/\sqrt7))^(\arctan(41/(3\sqrt7)))\sec^3z\,\mathrm dz`

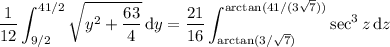
This is a fairly standard integral (it even has its own Wiki page, if you're not familiar with the derivation):


`\displaystyle\int\sec^3z\,\mathrm dz=\frac12\sec z\tan z+\frac12\ln|\sec x+\tan x|+C`

So the arc length is


`\displaystyle(21)/(32)\left(\sec z\tan z+\ln|\sec x+\tan x|\right)\bigg|_(z=\arctan(3/\sqrt7))^(z=\arctan(41/(3\sqrt7)))=(21)/(32)\ln\left((41+4√(109))/(21)\right)+(41√(109))/(24)-\frac98`