Answer:
Ques 1)

- The domain of f times g is all real numbers.
Ques 2)
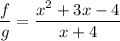
- All real numbers except x= -4
Explanation:
We are given two functions f(x) and g(x) as follows:
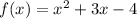
and
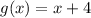
1)
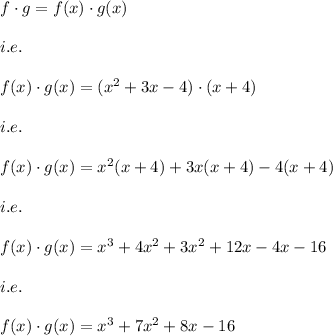
Also, we know that the polynomial function is defined everywhere,.
i.e. the domain of the polynomial function is all real numbers.
Hence, the domain of f times g is all real numbers.
2)
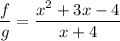
The function f/g is a rational function .
The domain of a rational function is all real numbers except the point where denominator is zero.
Hence, the domain of f/g is:
All real numbers except x= -4