Answer:
The volume of cone is 196 ft³.
Explanation:
As per given question we have provided that
 Diameter = 14 ft
Diameter = 14 ft
 Radius = 14/2 = 7 ft
Radius = 14/2 = 7 ft
 Height = 4 ft
Height = 4 ft
Here's the required formula to find the volume of cone :
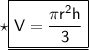
 V = Volume
V = Volume
 π = 3
π = 3
 r = radius
r = radius
 h = height
h = height
Substituting all the given values in the formula to find the volume of cone :
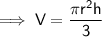
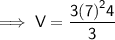
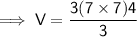
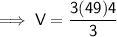
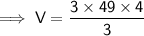
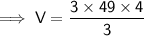
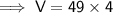
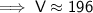
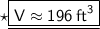
Hence, the volume of cone is 196 ft³.
