Question

Sam put $2,000 in a savings account at his bank. After 10 years, his account balance was $4,000. The interest rate on the savings deposit is

Answer 1

The answer is approx 7.1%

Explanation:

The compound interest formula is :

`A=p(1+r/n)^(nt)`

where, p = 2000

A = 4000

n = 1 (we will assume)

t = 10

r = ?

Now putting the values in formula we get

`4000=2000(1+r/1)^(10)`

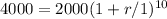
or

`2=(1+r)^(10)`

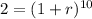
Switching sides:

`(1+r)^(10)=2`

`1+r=\sqrt[10]{2}`

Solving this we get, r=0.07177 and r=-2.07177(neglect the negative)

So, we have r=0.0717 ≈ 0.071 (taking only up to 3 decimal places)

And in percentage, this is 7.1%(approx)

Answer 2

`\bf ~~~~~~ \textit{Simple Interest Earned Amount} \\\\ A=P(1+rt)\qquad \begin{cases} A=\textit{accumulated amount}\dotfill & \$4000\\ P=\textit{original amount deposited}\dotfill & \$2000\\ r=rate\to r\%\to (r)/(100)\\ t=years\dotfill &10 \end{cases} \\\\\\ 4000=2000(1+r\cdot 10)\implies \cfrac{4000}{2000}=10r+1\implies 2=10r+1 \\\\\\ 1=10r\implies \cfrac{1}{10}=r\implies 0.1=r\implies \stackrel{\textit{converting to percentage}}{0.1\cdot 100\implies }~~\stackrel{\%}{10}=r`