Question

Given a and b are the first-quadrant angles, sin a=5/13, and cos b=3/5, evaluate sin(a+b)1) -33/652) 33/653) 63/65

Answer 1

We know that angles a and b are in the first quadrant. We also know this values:

`\begin{gathered} \sin a=(5)/(13) \\ \cos b=(3)/(5) \end{gathered}`

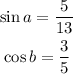
We have to find sin(a+b).

We can use the following identity:

`\sin (a+b)=\sin a\cdot\cos b+\cos a\cdot\sin b`

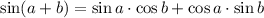
For the second term, we can replace the factors with another identity:

`\sin (a+b)=\sin a\cdot\cos b+\sqrt[]{1-\sin^2a}\cdot\sqrt[]{1-\cos^2b}`

Now we know all the terms from the right side of the equation and we can calculate:

`\begin{gathered} \sin (a+b)=\sin a\cdot\cos b+\sqrt[]{1-\sin^2a}\cdot\sqrt[]{1-\cos^2b} \\ \sin (a+b)=(5)/(13)\cdot(3)/(5)+\sqrt[]{1-((5)/(13))^2}\cdot\sqrt[]{1-((3)/(5))^2} \\ \sin (a+b)=(15)/(65)+\sqrt[]{1-(25)/(169)}\cdot\sqrt[]{1-(9)/(25)} \\ \sin (a+b)=(15)/(65)+\sqrt[]{(169-25)/(169)}\cdot\sqrt[]{(25-9)/(25)} \\ \sin (a+b)=(15)/(65)+\sqrt[]{(144)/(169)}\cdot\sqrt[]{(16)/(25)} \\ \sin (a+b)=(15)/(65)+(12)/(13)\cdot(4)/(5) \\ \sin (a+b)=(15)/(65)+(48)/(65) \\ \sin (a+b)=(63)/(65) \end{gathered}`

Answer: sin(a+b) = 63/65