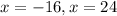we have
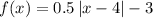 -----> equation A
-----> equation A
 -----> equation B
-----> equation B
equate equation A and equation B
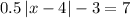
Adds
 boths sides
boths sides
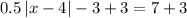
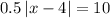
Multiply by
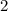 boths sides
boths sides
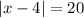
we know that
The function absolute value has two solutions
Step 1
Find the first solution (positive case)
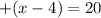
Adds
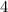 boths sides
boths sides
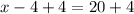

Step 2
Find the second solution (negative case)
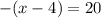
Multiply by
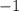 boths sides
boths sides
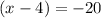
Adds
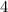 boths sides
boths sides
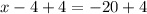
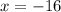
therefore
the answer is the option B