Answer:
1.275
Step-by-step explanation:
The given equation is:
f(x) = 0.01(2)ˣ
We want to find the rate of change from 2 to 10 which means that we need to find the slope from 2 to 10.
We start by getting the y-values for each of the given x-values:
at x = 2 ..........> y = 0.01(2)² = 0.04 ...........> point is (2, 0.04)
at x = 10 .........> y = 0.01(2)¹⁰ = 10.24 .........> point is (10, 10.24)
Now, we get the slope as follows:
slope =
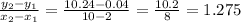
Hope this helps :)