Remember that a function is a relation between two sets of numbers where the first set is called domain, and the second set is called range.
The main characteristic that defines a function is that a domain element can be associated with only one element of the range set. In other words, one input value cannot have two different output values.
Therefore, the right answer is the third choice
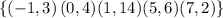
Because this represents a function and its inverse also represents a function, that is, it's inverse have the characteristic of a function. The following set represents the inverse
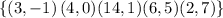
As you can observe, this inverse set also follows the function definition, because every single input is associated with only one output.