Question

I don't know how to start this. This is for Calc 1

Answer 1

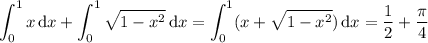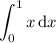
`\displaystyle\int_0^1x\,\mathrm dx` corresponds to the area under the curve
`y=x` from 0 to 1. This region is a right triangle with base and height 1, so the area of the triangle, and thus the value of the integral, is
`\frac12*1*1=\frac12`.


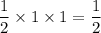
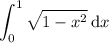
`\displaystyle\int_0^1√(1-x^2)\,\mathrm dx` is the area of one quadrant of the unit circle. Recall that
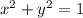
`x^2+y^2=1` is the equation of the circle with radius 1 centered at the origin. Solving for
`y` gives
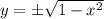
`y=\pm√(1-x^2)`, where the positive root corresponds to the top half of the circle. The top half is defined over the interval
`[-1,1]`, but you're only interested in the right half,
`[0,1]`. So this area is
`\frac14\pi*1^2=\frac\pi4`.

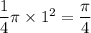
Put these together to get


`\displaystyle\int_0^1x\,\mathrm dx+\int_0^1√(1-x^2)\,\mathrm dx=\int_0^1(x+√(1-x^2))\,\mathrm dx=\frac12+\frac\pi4`