Question

Use graph paper and a straightedge to draw the figure. The set of points (–1, 2), (5, 2), (5, –4), and (–1, –4) identifies the vertices of a quadrilateral

Answer 1

Can you plot these four points as a start?

Answer 2

Answer with explanation:

The four vertices of a two dimensional geometrical shape are set of points A(–1, 2), B(5, 2),C (5, –4), and D(–1, –4).

Now plotting it on X Y plane

Point of intersection of Diagonals that is AC and B D given by the formula

`{\text{Mid point of AC}}=[(x_(1)+x_(2))/(2),(y_(1)+y_(2))/(2)]\\\\=[(-1+5)/(2),(-4+2)/(2)]\\\\=(2,-1)\\\\{\text{Mid point of BD}}=[(5-1)/(2),(2-4)/(2)]=(2,-1)`

Distance formula between two points in two dimensional plane

`=\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2}`

`AB=√((5+1)^2+(2-2)^2)=6\\\\BC=6\\\\CD=6, \\\\DA=6`

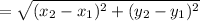
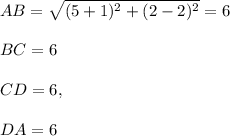
So, the Quadrilateral is Rhombus,because all sides are equal.

Slope of line between two points is given by

`=(y_(2)-y_(1))/(x_(2)-x_(1))`

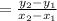
Slope of AB

`=(2-2)/(5+1)=(0)/(6)`

Slope of BC

`=(-4-2)/(5-5)=(-6)/(0)`

Product of slopes = -1

Hence ∠ABC=90°

If in a rhombus one angle measures 90°,then it a Square.

So, Above Quadrilateral with given vertices is a Square.