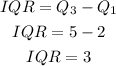Question

5. The number of hours spent in an airplane on a single flight is recordedon a dot plot. The mean is 5 hours. The median is 4 hours. The IQR is 3hours. The value 26 hours is an outlier that should not have been includedin the data. When 26 is removed from the data set, calculate the following(some values may not be used):*H0 2 4 6 8 10 12 14 16 18 20 22 24 26 28number of hours spent in an airplane1.4 hours1.5 hours3 hours3.5 hoursWhat is themean?OWhat is themedian?оOOWhat is the IQR?OOOO

Answer 1

The mean is 5 hours, the median is 4 hours, and the IQR is 3 hours.

Step-by-step explanation:

The mean is the average of a set of data. To find the mean, we sum up all the numbers in the data set and divide by the number of data points. In this case, the mean is 5 hours.

The median is the middle value of a data set when it is arranged in numerical order. In this case, the median is 4 hours.

The IQR (interquartile range) is a measure of the spread of the middle 50% of the data. It is calculated by subtracting the first quartile (Q1) from the third quartile (Q3). In this case, the IQR is 3 hours.

Answer 2

Since the outlier that is 26 has been removed

We will work with the remaining

Where X denotes the number of hours, and f represent the frequency corresponding to eaxh hours

We find the mean

The mean (X bar) is given by

`\begin{gathered} mean=(\Sigma fx)/(\Sigma f) \\ mean=(1(2)+2(2)+3(3)+4(3)+5(2)+6(2))/(2+2+3+3+2+2) \\ mean=(2+4+9+12+10+12)/(2+2+3+3+2+2) \\ mean=(49)/(14) \\ mean=(7)/(2) \\ mean=3.5 \end{gathered}`

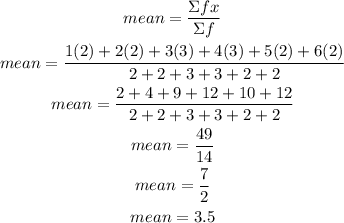
We now find the median

Median is the middle number

Since the total frequency is 14

The median will be on the 7th and 8th term in ascending order

`\begin{gathered} median=(7th+8th)/(2) \\ median=(3+4)/(2) \\ median=(7)/(2) \\ median=3.5 \end{gathered}`

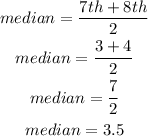
Lastly, we will find the interquartile range

The formula is given by

`IQR=Q_3-Q_1`

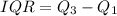
Where

`\begin{gathered} Q_3=(3)/(4)(n+1)th\text{ term} \\ Q_1=(1)/(4)(n+1)th\text{ term} \end{gathered}`

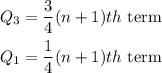
We calculate for Q1 and Q3

`\begin{gathered} Q_1=(1)/(4)(n+1)th\text{ term} \\ \text{n is the total frequency} \\ n=14 \\ Q_1=(1)/(4)(14+1)th\text{ term} \\ Q_1=(1)/(4)(15)th\text{ term} \\ Q_1=3.75th\text{ term} \\ Q_1\text{ falls betwe}en\text{ the frequency 3 and 4 in ascending order} \\ \text{From the table above} \\ Q_1=2 \end{gathered}`
`\begin{gathered} Q_3=(3)/(4)(n+1)th\text{ term} \\ Q_3=(3)/(4)(14+1)th\text{ term} \\ Q_3=(3)/(4)(15)th\text{ term} \\ Q_3=11.25th\text{ term} \\ \text{From the table above} \\ Q_3=5 \end{gathered}`

Therefore, the IQR is

`\begin{gathered} IQR=Q_3-Q_1 \\ IQR=5-2 \\ IQR=3 \end{gathered}`