Question

Find the vertices and foci of the hyperbola with equation x squared over sixteen minus y squared over forty eight = 1.

Answer 1

`\bf \cfrac{(x-{{ h}})^2}{{{ a}}^2}-\cfrac{(y-{{ k}})^2}{{{ b}}^2}=1 \qquad center\ ({{ h}},{{ k}})\qquad vertices\ ({{ h}}\pm a, {{ k}}) \\ \quad \\\\ foci\to h\pm c\quad where\quad c=√(a^2+b^2)\to h\pm √(a^2+b^2)\\ ----------------------------\\ \textit{now, let's see your hyperbola} \\ \quad \\ \cfrac{x^2}{16}-\cfrac{y^2}{48}=1\implies \cfrac{(x-0)^2}{4^2}-\cfrac{(y-0)^2}{(√(48))^2}=1`

and surely, you can see where the center is at, thus what h,k are,
and what "a" and "b" components are as well :)

Answer 2

Vertices are (4,0),(-4,0).

Foci are (8,0), (-8,0).

Explanation:

Given : The hyperbola equation
`(x^2)/(16)-(y^2)/(48)=1`

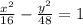
To find : The vertices and foci of the hyperbola ?

Solution :

The general form of the hyperbola equation is

`\cfrac{(x-{{ h}})^2}{{{ a}}^2}-\cfrac{(y-{{ k}})^2}{{{ b}}^2}=1`

Where, (h,k)=(0,0) is the center.

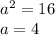`a^2=16\\a=4` and
`b^2=48\\b=√(48)`

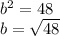
The vertices of the hyperbola is,

`V=(h\pm a,k)`

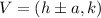
Substitute the value,

`V=(0\pm 4,0)`

`V=(4,0),(-4,0)`

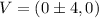
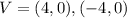
Therefore, Vertices are (4,0),(-4,0).

Foci is
`F=(\pm c,0)`

Where,
`c=√(a^2+b^2)`

`c=\sqrt{4^2+√(48)^2}`

`c=√(16+48)`

`c=√(64)`

`c=8`

`F=(\pm 8,0)`

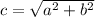
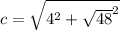
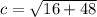
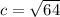
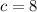
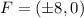
Therefore, Foci are (8,0), (-8,0).