Question

Determine whether the vectors u and v are parallel, orthogonal, or neither.

u = <10, 6>, v = <9, 5>

Answer 1

`\mathbf u\cdot\mathbf v=\|\mathbf u\|\|\mathbf v\|\cos\theta`

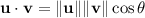
where
`\theta` is the angle between the vectors. You have


`10*9+6*5=√(10^2+6^2)√(9^2+5^2)\cos\theta\iff \cos\theta=(30)/(√(901))\implies \theta\approx1.909^\circ`

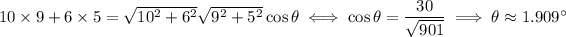
The vectors would be orthogonal if the dot product had been zero, but that's clearly not the case.

They would be parallel if the angle turned out to be
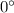
`0^\circ` or
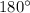
`180^\circ`, but that's also not the case.

So the answer is neither.