Answer:
Third option is correct.
Explanation:
The given table is
x f(x)
–6 1
–3 2
2 5
5 3
8 0
If the coordinates of a function f(x) is defined as (x,y), then the coordinates of inverse of f(x) is defined as (y,x).

![[\because g(x)=(y,x)]](https://img.qammunity.org/2018/formulas/mathematics/college/t8rnoggmvq268j67ppz5zfa2cxbb92o0cg.png)
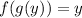
![[\because f(x)=(x,y)]](https://img.qammunity.org/2018/formulas/mathematics/college/uvqh9e53pfrpzbx0bt65iofih2o352hip6.png)
If g(x) is the inverse of f(x), then the value of f(g(y)) is y.
It is given that g(x) is the inverse of f(x), then the value of f(g(2)) is 2.
Therefore third option is correct.