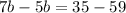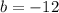Question

The axis of symmetry for the graph of the function is f(x) = x2 + bx + 10 is x = 6. What is the value of b?

Answer 1

`b=-12`

Explanation:

we have

`f(x)=x^(2)+bx+10`

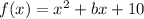
we know that

The equation of a vertical parabola into vertex form is equal to

`y=a(x-h)^(2) +k`

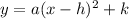
where

(h,k) is the vertex of the parabola

and the axis of symmetry is equal to
`x=h`

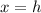
In this problem we have the axis of symmetry
`x=6`

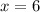
so

the x-coordinate of the vertex is equal to
`6`

therefore

For
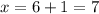`x=6+1=7` -----> one unit to the right of the vertex

Find the value of
`f(7)`

`f(7)=7^(2)+b(7)+10`

`f(7)=59+7b`

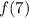
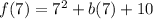
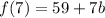
For
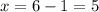`x=6-1=5` -----> one unit to the left of the vertex

Find the value of
`f(5)`

`f(5)=5^(2)+b(5)+10`

`f(5)=35+5b`

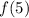
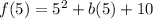
Remember that

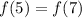`f(5)=f(7)` ------> the x-coordinates are at the same distance from the axis of symmetry

so

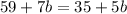`59+7b=35+5b` ------> solve for b

`7b-5b=35-59`

`2b=-24`

`b=-12`