Question

(PYTHAGOREAN THEOREM)

A diagonal of a cube goes from one of the cube's top corners to the opposite corner of the base of the cube. Find the length to a diagonal d in a cube that has an edge of length 10 meters.

Answer 1

First draw a picture (see attached).

You want to find the diagonal of the cube, length AB.
The right triangle formed is trianagle ABD.
AD = 10m

DB will be the hypotenuse of triangle BCD.

`(BC)^2 + (CD)^2 = (DB)^2 \\ (10)^2 + (10)^2 = (DB)^2 \\ DB = √(200)= 10 √(2)`.

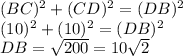
If we know the length of AD and DB, we can find AB.

`(AD)^2+(BC)^2 = (AB)^2 \\ (10)^2 + (10 √(2))^2 = (AB)^2 \\ AB = √(300) = 10 √(3)`

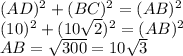In fact, the diagonal of any cube is √3 times the side length of the cube.
Let s be the side length (as in AD or CD in the attached) and
h be the hypotenuse of the base, (DB in the attached) and
d be the diagonal of the cube (AB in the attached).

The hypotenuse of the base will be:
`s^2+s^2 = h^2 \\`.

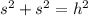
The cube's diagonal will be:

`h^2+s^2 = d^2`.

Substituting
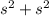
`s^2+s^2` as
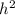
`h^2`, you have

`s^2+s^2+s^2 = d^2 \\ 3s^2 = d^2 \\ d = √(3s^2) = s√(3)`