Question

A 12 sided die is rolled. the set of equally likely outcomes is { 1,2,3,4,5,6,7,8,9,10,11,12}. find the probability of rolling a number greater than 8.

Answer 1

The probability of rolling a number greater than 8 is 1/3.

Step-by-step explanation:

To find the probability of rolling a number greater than 8, we need to determine the number of favorable outcomes and divide it by the total number of equally likely outcomes. In this case, the favorable outcomes are {9, 10, 11, 12} since these numbers are greater than 8. The total number of equally likely outcomes is 12, as given in the question.

Therefore, the probability of rolling a number greater than 8 is:

Probability = Number of favorable outcomes / Total number of equally likely outcomes = 4 / 12 = 1/3

Answer 2

Answer : The probability rolling a number greater than 8 is,
`(1)/(3)`

Step-by-step explanation :

Probability : It is defined as the extent to which an event is likely to occur. That means, it is measured by the ratio of the favorable outcomes to the total number of possible outcomes.

`\text{Probability}=\frac{\text{Number of favorable outcomes}}{\text{Total number of favorable outcomes}}`

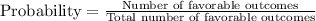
Favorable outcomes are, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

Now we have to calculate the probability rolling a number greater than 8.

Favorable outcomes rolling a number greater than 8 are, 9, 10, 11, 12

Number of favorable outcomes rolling a number greater than 8 = 4

Total number of outcomes = 12

`\text{Probability}=\frac{\text{Number of favorable outcomes rolling a number greater than 8}}{\text{Total number of favorable outcomes}}`

`\text{Probability}=(4)/(12)`

`\text{Probability}=(1)/(3)`

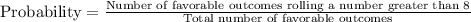
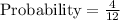
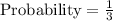
Thus, the probability rolling a number greater than 8 is,
`(1)/(3)`