Question

What is the solution to the system of linear equations represented by the matrix below?

[2 4] [x] = [6]
[1 2] [y] [3]
A. x= 3 , y= 0
B. x= 0 , y= 3/2
C. The system of equations has no solution
D. The system of equations has infinite solutions

Answer 1

D. The system of equations has infinite solutions.

Explanation:

Given system of equations,

`\begin{bmatrix}2 & 4 \\ 1 & 2\end{bmatrix}.\begin{bmatrix}x\\ y\end{bmatrix}=\begin{bmatrix}6\\ 3\end{bmatrix}`

`\implies \begin{bmatrix}2x+4y\\ x+2y\end{bmatrix}=\begin{bmatrix}6\\ 3\end{bmatrix}`

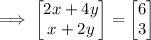
By comparing both sides,

We get,

2x + 4y = 6,

x + 2y = 3,

We know that a system
`a_1x+b_1y=c_1`,
`a_2x+b_2y=c_2`

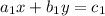has a unique solution if,

`(a_1)/(a_2)\\eq (b_1)/(b_2)\\eq (c_1)/(c_2)`

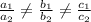
No solution, if,

`(a_1)/(a_2)=(b_1)/(b_2)\\eq (c_1)/(c_2)`

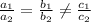
Infinitely many solution if,

`(a_1)/(a_2)=(b_1)/(b_2)=(c_1)/(c_2)`

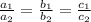
Here,

`(2)/(1)=(4)/(2)=(6)/(3)=2`

Hence, the system of equation has infinite solutions.

Option D is correct.