Part A: Since triangle 2 is a right triangle, write an equation applying the Pythagorean Theorem to the triangle.
Triangle 2 has the following sides: a, b and n
Writing it into an equation will be:
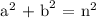
The answer is a² + b² = n²
Part B: Since the equations for both triangles have a^2 + b^2, you can think of the two equations for c^2 and n^2 as a system of equations. Substitute what a^2 + b^2 equals in the first equation for a^2 + b^2 in the second equation. After you substitute, what equation do you get?
Equation 1 (Triangle 1): a² + b² = c²
Equation 2 (Triangle 2): a² + b² = n²
Substitute what a^2 + b^2 equals in the first equation for a^2 + b^2 in the second equation, it will be:
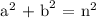
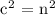
The answer is c² = n²
Part C : Now, take the square root of both sides of the equation from part B and write the resulting equation.
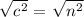

The answer is c = n