Answer:
Option 1 must be true .i.e., Slope of TR is 5
Explanation:
Given: Δ MNO ≅ Δ RST
∠R = 90°
Slope of RS =
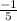
We are given ΔMNO is congruent to ΔRST but we are not told which side is equal to which side.
Means in ΔRST we know ∠R is right angle but in ΔMNO we dont know which angle is right angle.
⇒ We can't say anything about slopes of sides of ΔMNO.
Therefore, Option 2 , 3 , 4 can be true but not sure.
But, in ΔRST
∠R is right angle means RS ⊥ RT
Slope of RS,
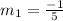
Let Slope of RT be
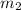
We know that product of slopes of perpendicular lines are equal to -1.
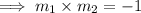
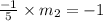
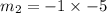
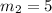
Therefore, Option 1 must be true .i.e., Slope of TR is 5