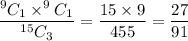Question

A jar contains 6 chocolate chip cookies and 9 peanut butter cookies. Richard grabs 3 cookies at random to pack in his lunch. What is the probability that he drew 2 chocolate chip cookies and 1 peanut butter cookie?

A.
`(1)/(54)`

B.
`(1)/(27) }`

C.
`(9)/(91) }`

D.
`(27)/(91) }`

Answer 1

Here, Your Answer would be 9/91

In short, Answer is Option C

Hope this helps!

Answer 2

Answer: D.
`(27)/(91)`

Explanation:

Given: Number of chocolate chip cookies - 6

Number of peanut butter cookie = 9

Total cookies = 6+9=15

The total number of combinations of selecting 3 cookies from 15 cookies

`^(15)C_3=(15!)/((15-3)!3!)=455`

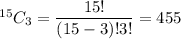
The number of combinations to select 2 chocolate chip cookie=

`^(6)C_2(6!)/((6-2)!2!)=15`

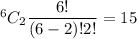
The number of combinations to select 1 peanut butter cookie=

`^(9)C_1=(9!)/((9-1)!1!)=9`

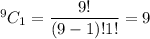
The probability that he drew 2 chocolate chip cookies and 1 peanut butter cookie=
`(^(9)C_1* ^(9)C_1)/(^(15)C_3)=(15*9)/(455)=(27)/(91)`