Question

Please help me with this! (Sadly my previous tutor couldn't help me with this)

Answer 1

a.

The free body diagram (not at scale) for each crate is shown below:

b.

In this case we know that the force is just sufficient to keep the crates from sliding, this means that the acceleration of the system is zero.

From the free body diagram and Newton's second law we have that for the 45 kg crate that:

`\begin{gathered} T-W=0 \\ T=W \\ T=(45)(9.8) \\ T=441 \end{gathered}`

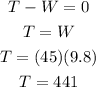
For the 35 kg crate the equations of motion would be:

`\begin{gathered} F+f_f-T=0 \\ N-W^(\prime)=0 \end{gathered}`

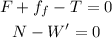
but we know that the force of friction is given by:

`F_f=\mu N`

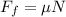
and from the second equation of motion we have that:

`\begin{gathered} N=W^(\prime) \\ N=(35)(9.8) \\ N=343 \end{gathered}`

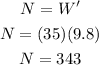
Then we have that:

`\begin{gathered} F+F_f-T=0 \\ F+343\mu-441=0 \end{gathered}`

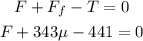
Since the crates are not moving we need to use the static coefficient of friction, then:

`\begin{gathered} F+343\mu-441=0 \\ F+343(0.5)-441=0 \\ F+171.5-441=0 \\ F-269.5=0 \\ F=269.5 \end{gathered}`

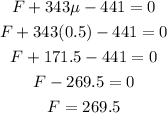
Therefore the force applied is 269.5 N

c.

The diagram in this case is:

d.

In this case we know that the 35 kg is sliding to the right at constant velocity, this means that the acceleration for the system is zero. (Notice that the difference with the previous case is that the friction points to the left)

From the discussion in part b we know that for the 45 kg block:

`T-W=0`

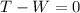
and then:

`T=441`

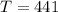
For the 35 kg we have that:

`\begin{gathered} F-F_f-T=0 \\ N-W^(\prime)=0 \end{gathered}`

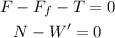
from the previos discussion we know that:

`N=343`

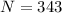
and since in this case the crates are moving we need to use the kinetic coefficient of friction, then we have:

`\begin{gathered} F-F_f-T=0 \\ F-(0.3)(343)-441=0 \\ F-102.9-441=0 \\ F-543.9=0 \\ F=543.9 \end{gathered}`

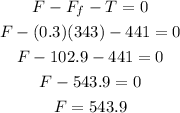
Therefore in this case the force applied is 543.9 N

e.

In this case the free body diagram is:

f.

Since the crates are moving with an accelearion of 0.5 m/s^2 we have for the 45 kg crate that:

`T-W=ma`

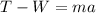
from where:

`\begin{gathered} T-(9.8)(45)=(45)(0.5) \\ T-441=22.5 \\ T=441+22.5 \\ T=463.5 \end{gathered}`

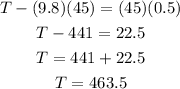
For the 35 kg crate we have that:

`\begin{gathered} F-F_f-T=m^(\prime)a \\ N-W^(\prime)=0 \end{gathered}`

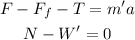
from the previous discussion we know that N=343, plugging this in the first equation we have:

`\begin{gathered} F-(0.3)(343)-463.5=(35)(0.5) \\ F-102.9-463.5=17.5 \\ F-566.4=17.5 \\ F=566.4+17.5 \\ F=583.9 \end{gathered}`

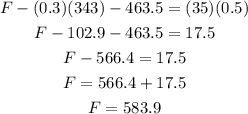
Therefore the force applied in this case is 583.9 N